Il modulo di rilevazione e correzione dell'intensità della luce

Il modulo MLU computa il valore di illuminazione medio dei due pattern sensoriali, lo confronta con l'illuminazione media dei pattern di addestramento della rete e corregge l'eccesso di attivazione sulle matrici di Kohonen, per filtrarle di ogni componente che non siano quelle relative alle caratteristiche spaziali della fonte di luce.

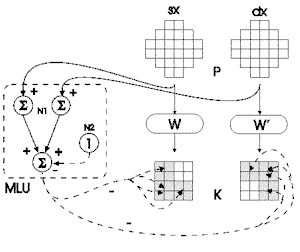
Figura 1. Modulo di calcolo dell'intensità globale della luce MLU. Il neurone N2 ha un valore pari alla intensità luminosa di base, quella cioè dei pattern di esempio. I neuroni di ingresso N1 e quello di uscita del modulo hanno funzioni di trasferimento tali per cui l'attivazione di uscita è la media di quelle di entrata.

L'informazione mappata sulla matrice di Kohoneni binoculare è analogica a quella spaziale reale; vediamo ora se ed in che modo è analogica all'intensità della luce che colpisce i due occhi. Fino ad ora, infatti, avevamo considerato dei pattern i cui recettori avevano valore zero se appartenevano alla zona in ombra e uno se si trovavano nella zona illuminata e valori intermedi, proporzionali alla quantità di luce che colpiva ogni singolo recettore, nelle zone di confine fra luce ed ombra.
Proviamo a considerare il fatto che la luce abbia intensità variabile: una luce più intensa determinerà un innalzamento sia del valore dei recettori esposti direttamente ad essa nella zona illuminata, sia di quelli della zona in ombra, per il fenomeno della diffusione della luce. Anche se ciò non corrisponde esattamente a quello che capita nella realtà, per ragioni legate alla chiarezza espositiva, si assume che l'aumento del valore dei recettori della zona di luce sia equivalente a quello dei recettori della zona d'ombra e, quindi, la differenza massima fra il valore del recettore più attivo e quello meno attivo sia sempre uno; allo stesso modo assumiamo che tale aumento sia equivalente anche nei recettori che occupano posizioni di confine fra la zona illuminata e la zona in ombra della sfera formata dai due occhi.
Un'ipotesi che si può formulare, date le caratteristiche delle matrici di Kohonen, è che l'energia totale dei recettori abbia una ripercussione immediata sulle mappe delle matrici. In altre parole aumentando la luce totale aumenterebbe anche il valore delle attivazioni delle matrici di Kohonen. Per un'altra caratteristica della rete di Kohonen, cioè quella di avere i neuroni con una funzione di trasferimento lineare, ci si può aspettare che non solo aumenta l'attivazione dei neuroni delle matrici aumentando l'intensità della fonte di luce, ma che tale aumento è proporzionale all'incremento dell'intensità in modo lineare.

Nei sistemi biologici esistono delle connessioni dirette fra la retina ed alcuni centri non specifici per la funzione visiva: Per esempio fra la retina ed il nucleo soprachiasmatico che sembra che siano importanti per sincronizzare i cicli circadiani con il ciclo luce-buio. E' plausibile pensare, pertanto, che queste connessioni portino informazioni relative alla luce totale diffusa. Ancora una volta proviamo ad emulare i sistemi biologici e costruiamo delle connessioni dirette fra i recettori della retina ed un modulo che ne estragga l'informazione relativa alla luce diffusa.

Procedura per la normalizzazione delle matrici di Kohonen rispetto alla luce

1. Si calcola la media dell'attivazione dei recettori per ognuno dei due pattern sensoriali; 2. Si calcola la media delle medie relative ai due pattern e si trova, in tal modo, la luminosità globale. 3. Si sottrae la luminosità di base relativa ai pattern di addestramento (che ha valore 1) alla luminosità attuale; 4. si inibiscono (si sottrae da) le componenti delle matrici di Kohonen di una quantità equivalente a quella calcolata al punto 3.

La procedura completa per correggere le matrici ed eliminare dalle sue componenti l'attivazione "intrusa" relativa all'intensità della luce è descritta sopra. In generale si può dire che il principio di funzionamento della correzione è il calcolo dell'attivazione globale dei recettori, il confronto con l'attivazione di base e l'inibizione sui neuroni delle matrici di una quantità pari alla differenza fra l'attivazione globale attuale e quella di base relativa ai pattern di addestramento per le matrici di Kohonen.
L'architettura del modulo in questione è illustrata nella figura 1 MLU. I neuroni di ingresso N1 di tale modulo ricevono l'eccitazione proveniente da tutti i recettori del pattern sensoriale relativo, le somma e le trasferisce in uscita con un valore che è un ventiquattresimo della sua attivazione: questa funzione di trasferimento restituisce in uscita di ogni neurone N1 la media degli ingressi costituiti dai recettori sensoriali, che sono appunto 24 per ogni pattern. Anche il neurone di uscita, che trasferisce la metà del valore di ingresso, fa la media delle attivazioni di input; l'inibizione di 1 del neurone N2 il cui valore sta per l'intensità di base, quella cioè relativa ai pattern di addestramento delle reti di Kohonen W e W', è proprio sul valore trasferito dal neurone. Il valore risultante sarà il valore delle connessioni inibitorie sulle componenti attive delle matrici (figura 1, K).