| |
 |
|
|
|
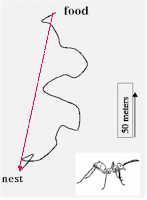
ANT
MODELLO
VETTORIALE
|
|
|
 |
 |
|
|
 |
|
|
|
 |
il
MODELLO VETTORIALE è l'insieme delle
abilità (che verranno IMPLEMENTATE nel
sistema di controllo di ANT) sufficienti
per il comportamento di homing di un agente che si orienta in base ad
una fonte di luce e consente di stimare:
|
|
|
 |
|
|
 |
|
|
|
 |
1 |
la
DIREZIONE che dovrebbe avere
la luce (o la luce polarizzata) rispetto al sistema di riferimento egocentrico
(dal punto di vista dell'agente) perché l'agente sia allineato con
la direzione del punto di partenza; |
|
|
|
 |
|
|
 |
|
|
 |
|
|
|
 |
2 |
la
DISTANZA fra il punto
attuale ed il punto di partenza. |
| |
 |
| |
|
|
| |
|
Vedremo
ora la descrizione dettagliata dell MODELLO VETTORIALE
|
| |
|
RICORDIAMO
CHE:
|
| |
|
|
| |
|
L'AGENTE
COLLOCA SE' STESSO NELLO SPAZIO RISPETTO ALLA FONTE DI LUCE. |
| |
|
|
| |
|
LA
DIREZIONE DELLA LUCE E' DA CONSIDERARSI PARALLELA
IN OGNI PUNTO (così come la direzione del piano polarizzato determinato
dalla luce del sole per la formica del deserto)
|
| |
|
|
| |
|
|
| |
|
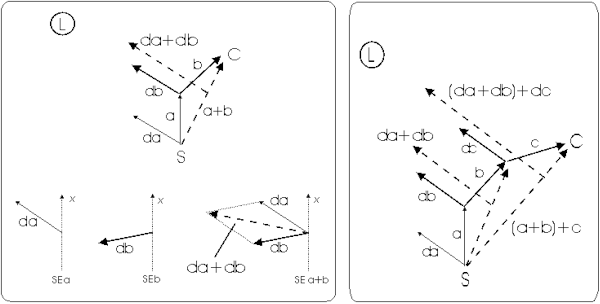
Figura
1. Riquadro a sinistra: traiettoria di
due vettori. S: fonte di luce proiettata sul piano bidimensionale
dell'agente. SE: sistema di riferimento egocentrico. d: direzione
della fonte di luce rispetto al sistema di riferimento egocentrico. Riquadro
a destra: proprietà associativa applicata alla somma vettoriale
delle direzioni della fonte di luce in traiettorie con più di due
vettori.
|
| |
|
|
| |
|
Si consideri la
figura 1. Il riquadro a sinistra mostra una traiettoria formata da
due vettori. In alto a sinistra con L è contrassegnata la fonte
di luce proiettata sul piano dell'azimut. La luce si trova ad una distanza
tale per cui la sua direzione può essere considerata parallela
in ogni punto del piano, proprio come l'azimut del sole. La parte in basso
del riquadro mostra le direzioni della fonte di luce rispetto al sistema
di riferimento egocentrico x, ovvero dal punto di vista dell'agente.
SEa è il sistema di riferimento egocentrico nell'istante
t=0, quando l'agente ha direzione a, mentre da è
la direzione della luce in quell'istante. Lo stesso dicasi per SEb.
SEa+b mostra come la direzione della luce rispetto al sistema di
riferimento egocentrico allineato con la direzione che collega il punto
di partenza con quello di arrivo, si ottiene sommando vettorialmente le
direzioni della luce rispetto agli altri due sistemi di riferimento (da
e db rispetto a SEa e SEb) allineati con le direzioni
dei due vettori a e b. La proprietà che consente
di fare ciò è la proprietà
commutativa della somma vettoriale o regola del parallelogramma.
Nel caso di traiettorie complesse formate da più di due vettori
(figura 1 - riquadro a destra), applicando la proprietà
associativa della somma vettoriale, in
ogni istante la somma è fra la direzione della fonte di luce attuale
e il vettore risultante dalla somma delle direzioni della luce degli istanti
precedenti, sempre rispetto al sistema di riferimento egocentrico.
|
| |
|
|
| |
|
Per
ritornare al punto di partenza l'agente dovrebbe allineare la percezione
attuale della fonte di luce, disponibile grazie al sistema percettivo,
con la risultante della somma vettoriale delle direzioni precedenti.
|
| |
|
|
| |
|
In questo modo però
avrebbe il punto di partenza alle sue spalle: ruotando di 180°
la direzione del vettore risultante della somma vettoriale delle direzioni
precedenti ed allineando successivamente quella attuale con essa, si
troverebbe con il punto di partenza dritto avanti a sé.
|
| |
|
|
| |
|
Basterebbe,
a questo punto, che procedesse mantenendo tale allineamento e giungerebbe
fino al punto di partenza.
|
| |
|
|
| |
|
Il vettore
risultante dalla somma associativa, sarà chiamato vettore aspettativa.
In effetti si tratta proprio di qualcosa di atteso, che non è presente
nella realtà percettiva, ma che è disponibile per essere utilizzato
per allinearsi con la direzione di ritorno. Il vettore che indica la direzione
della fonte di luce rispetto al sistema di riferimento egocentrico (da
e db in figura 1) sarà chiamato
vettore percezione, in quanto rappresenta la direzione della
fonte di luce così come è percepita. Il vettore che rappresenta
la direzione della traiettoria dell'agente in ogni istante sarà chiamato
vettore traiettoria. |
| |
|
|
| |
|
|
| |
|
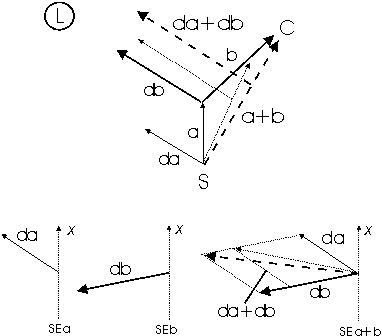
Figura
2. Il vettore aspettativa da+db dipende anche dalla norma
dei vettori da e db. Le righe sottili si riferiscono al
caso in cui i vettori traiettoria a e b abbiano norma uguale.
|
| |
|
|
| |
|
Fino ad
ora, si è supposto che la norma dei vettori direzione relativi agli
istanti discreti fosse sempre la stessa, ovvero che l'agente avesse la stessa
velocità in ogni istante. Si supponga ora che l'agente abbia velocità
variabile. Per questo è necessario aggiungere la velocità
al modello, espressa come norma del vettore traiettoria relativo ad un
determinato istante. A tal proposito si consideri la figura 2.
Essa mostra una traiettoria semplice, costituita da due vettori a
e b. La situazione è analoga a quella di figura 1,
riquadro in alto, ma questa volta il vettore b ha una norma maggiore
del corrispondente della figura 1. Si osservi come, mutando la norma
del vettore traiettoria b, muta la direzione del vettore aspettativa.
Pertanto la direzione del vettore aspettativa dipende anche dalla velocità
dell'agente; in altre parole la direzione della
fonte di luce a cui allinearsi per poter tornare al punto di partenza dipende,
oltre che dalla direzione della fonte di luce in ogni istante, rispetto
al sistema di riferimento egocentrico, anche dalla velocità dell'agente
in ogni istante, espressa come la norma
del vettore traiettoria (a, b), relativo a quell'istante.
La norma del vettore traiettoria in ogni istante (a, b), la velocità
effettiva dell'agente, sarà anche la norma del vettore percezione
nel medesimo istante (da, db). In tal modo la direzione del vettore
aspettativa (da+db) è direttamente influenzata dalla velocità,
come mostra la porzione Sea+b della figura 2 (linea tratteggiata).
Anche il valore della norma del vettore aspettativa è importante,
in quanto la somma fra tale vettore ed il vettore percezione successivo
è influenzata direttamente da essa come lunghezza di un lato del
parallelogramma, la cui diagonale sarà il vettore aspettativa successivo.
Si osservi, inoltre, che la norma del vettore aspettativa è direttamente
proporzionale alla norma del vettore a+b di figura 1 e 2,
proprio in base alla definizione della norma dei vettori percezione (da+db
in figura 1 e 2). Questo significa che il modello vettoriale
può stimare anche la distanza,
nel senso che, procedendo nella stessa direzione
la norma del vettore aspettativa aumenta, mentre procedendo nella direzione
opposta rispetto alla precedente la norma del vettore aspettativa diminuisce,
in quanto la direzione dei vettori percezione è opposta nei due casi.
|
| |
|
|
| |
|
|
| |
|
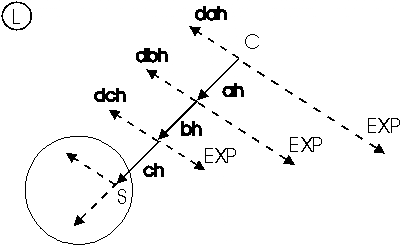
Figura
3. Quando l'agente inizia il percorso di homing dal punto attuale
C al punto di partenza S, la norma del vettore aspettativa
(EXP) diminuisce progressivamente, sommando in modo associativo
i vettori percezione (dah, dbh, dch) con l'avvicinamento al punto
di partenza S. ah, bh, ch: vettori traiettoria. dah,
dbh, dch: direzione della luce rispetto al sistema di riferimento
egocentrico (vettori percezione). EXP: vettore aspettativa.
|
| |
|
|
| |
|
Supponiamo
ora che l'agente debba tornare dal punto attuale al punto di partenza. Ha
a disposizione nella memoria locale la direzione a cui allinearsi per trovarsi
il punto di partenza di fronte (vettore aspettativa
ruotato di 180°); basterà che l'agente proceda mantenendo
tale allineamento per giungere al punto di partenza. Inoltre, il MODELLO
VETTORIALE consente anche di stimare la DISTANZA
RESIDUA dal punto di partenza. Come si vede in figura 3,
continuando a sommare il vettore percezione
(dah, dbh, dch, ...) durante il ritorno in modo associativo al vettore
aspettativa (EXP) la norma del vettore aspettativa diminuirà,
fino ad essere zero in prossimitò del punto di partenza (S). |
| |
|
|
| |
|
ALGORITMO
del modello vettoriale di homing.
|
| |
|
|
| |
|
1
|
Nell'istante
t=0 la direzione della fonte di luce a cui l'agente deve allinearsi per
avere il punto di partenza avanti a sé (vettore aspettativa) è
esattamente quella che percepisce ruotata di 180 gradi. La norma di tale
vettore è uguale a quella del vettore relativo alla traiettoria,
ovvero la velocità nell'istante t=0; |
| |
|
|
| |
|
2
|
nell'istante
t=1 la direzione del vettore aspettativa è il vettore direzione della
fonte di luce percepita nell'istante precedente (vettore percezione) sommata
vettorialmente a quello relativo alla direzione percepita nell'istante attuale.
La norma del vettore percezione è uguale alla norma del vettore relativo
alla traiettoria (vettore traiettoria), cioè alla velocità
dell'agente nell'istante t=1. La norma del vettore aspettativa è
uguale alla diagonale del parallelogramma i cui lati sono i due vettori
percezione. Anche in questo caso il vettore aspettativa deve essere ruotato
di 180 gradi perché l'agente, allineando la sua percezione della
direzione attuale della luce con quella del vettore aspettativa, si trovi
ad avere il punto di partenza davanti a sé. |
| |
|
|
| |
|
3
|
nell'istante
t=2, per la proprietà associativa della somma vettoriale, la direzione
del vettore aspettativa è il vettore aspettativa calcolato in t=1
più il vettore percezione nell'istante attuale t=2. La norma del
vettore percezione dell'istante t=2 è uguale alla norma del vettore
traiettoria, ovvero alla velocità nell'istante t=2. |
| |
|
|
| |
|
4
|
nell'istante t=n,
sempre per la proprietà associativa, la direzione del vettore aspettativa
attuale (t=n) è uguale alla somma vettoriale fra il vettore aspettativa
nell'istante t=n-1 e il vettore percezione che ha norma uguale alla norma
del vettore traiettoria, ossia la velocità nell'istante t=n.
|
| |
|
|
| |
|
|
|
|
|
©
2011 Emernet
|