L'allineamento con la direzione stimata

Tratterò qui del confronto delle matrici di rappresentazione visiva, reale e dell'homing, e di come sia possibile ricavare da tale confronto l'attivazione reciproca dei motoneuroni (SISTEMA MOTORIO) perchè ANT si allinei con la direzione attesa.

Il confronto delle matrici relative alla DIREZIONE PERCEPITA e dell'HOMING, infatti, si deve tradurre in componenti motorie (SISTEMA MOTORIO), ovvero in un'attivazione dei motoneuroni che faccia muovere l'agente in modo coerente rispetto a tale confronto.

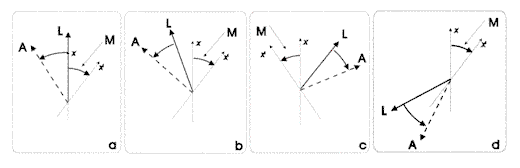
Figura 1. Esempi di rotazione del sistema di riferimento x per allineare la direzione reale (linea continua) con quella attesa (linea tratteggiata).

Analizziamo il problema dal punto di vista formale e consideriamo la figura 1. Allineare la percezione attuale L a quella virtuale A, significa ruotare il sistema di riferimento x di un angolo pari all'angolo formato dalle due direzioni, nel senso opposto a quello di tale angolo (M). In questo modo, nel nuovo sistema di riferimento ruotato x', la percezione reale coincide con quella virtuale nel vecchio sistema di riferimento x.
Se consideriamo il sistema di riferimento x della figura 1 come il sistema di riferimento egocentrico del nostro agente adattivo, possiamo dire che data la percezione reale attuale (matrice binoculare) e quella attesa virtuale (matrice di homing), l'agente deve compiere un movimento che lo faccia ruotare di un angolo pari a quello formato dalle due direzioni percepite. Il senso del movimento sarà quello contrario al verso dell'angolo, orientato dalla direzione reale a quella virtuale, come in figura 1.

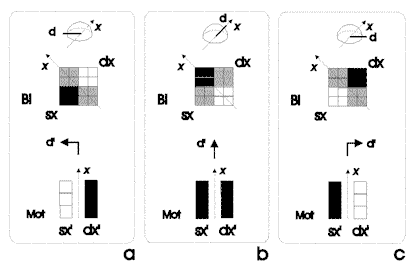
Figura 2. Analogia fra la matrice binoculare Bi ed il sistema motorio Mot. d: direzione della luce. d': spostamento dell'agente. sx, dx: componenti "destra" e "sinistra" della matrice binoculare la cui attivazione in relazione ad una direzione della fonte di luce d, è analogica all'attivazione dei neuroni rispettivamente della fila sinistra sx' e destra dx' del pattern motorio in relazione ad un movimento nella stessa direzione della luce, rispetto al sistema di riferimento egocentrico x.

Confronto e determinazione delle componenti motorie

Prima di tutto è necessario trovare un modo di coordinare la percezione visiva con l'attività dei motoneuroni. Osserviamo la figura 2. I tre riquadri mostrano l'analogia fra la matrice binoculare relativa ad una direzione e il pattern motorio. In particolare fra le componenti "destra" (dx) e "sinistra" (sx) di tale matrice le file di motoneuroni sinistra (sx') e destra (dx').
L'analogia è ancora più stretta se si pensa alla definizione dello spostamento in relazione all'attivazione dei motoneuroni di una fila rispetto all'altra: lo spostamento è massimo (90 gradi) quando i motoneuroni di una fila assumono valore uno e quelli dell'altra zero. Come si ricorderà anche la matrice binoculare ha la massima attivazione nella bolla relativa ad una delle direzioni cardinali, quando la fonte di luce proviene da una di queste direzioni, ed il valore di tale attivazione è proprio uno. Si può generalizzare affermando che all'attivazione delle componenti "destra" (dx) e "sinistra" (sx) della matrice binoculare relative ad una determinata direzione d della fonte di luce rispetto al sistema di riferimento egocentrico x, corrisponde rispettivamente un'attivazione della fila sinistra (sx') e destra (dx') del pattern dei motoneuroni, relativa ad un movimento d' nella stessa direzione di d.

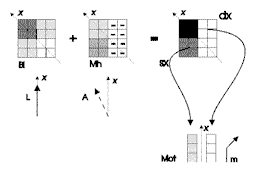
Figura 3. Sommando la matrice binoculare Bi, relativa alla direzione della luce attuale così come è percepita, alla matrice dell'homing Mh (attesa) si ottiene una matrice, le cui componenti "destra" (dx) e "sinistra" (sx) sono informative per quello che riguarda il movimento da mettere in atto per allineare L (reale) ad A (attesa).

In effetti, se si considera il discorso speculare, ad un determinato movimento dell'agente in una direzione corrisponde uno spostamento della fonte di luce in senso opposto, rispetto al sistema di riferimento egocentrico, dato che abbiamo supposto che la sua proiezione sul piano dell'azimut sia fissa. Lo spostamento della direzione della luce rispetto al sistema di riferimento egocentrico è sicuramente coerente con lo spostamento e questo si rifletterà direttamente, in maniera topologica, sulla matrice binoculare.
Abbiamo quindi trovato gli indici che ci servivano: il collegamento fra sistema motorio e sistema visivo sta proprio nell'analogia fra le componenti dx e sx della matrice binoculare e quelle sx' e dx' del sistema motorio (figura 2).
Consideriamo ora la figura 3. Essa illustra la situazione del riquadro a della figura 1, dal punto di vista della matrice binoculare (Bi) e dell'homing (Mh). Si osservi come, in tale condizione, sommando le due matrici e trasferendo successivamente l'attivazione delle componenti "destra" e "sinistra" della matrice risultante rispettivamente sulla fila destra e sinistra dei motoneuroni del sistema motorio Mot, si determina uno spostamento m coerente con l'allineamento della percezione reale L e attesa A, ovvero nella stessa direzione di A rispetto a L, ma in senso opposto. In questo modo lo spostamento m fa in modo di avvicinare la percezione reale della direzione della luce con quella che si dovrebbe avere (attesa). In questo caso, qualsiasi sia la direzione attesa, il pattern motorio si ottiene sommando le due matrici binoculare e dell'homing e trasferendo l'attivazione delle componenti "destra" e "sinistra" della matrice ottenuta, che da ora innanzi chiameremo matrice visuo-motoria, sulle file dei motoneuroni, nel modo descritto sopra.

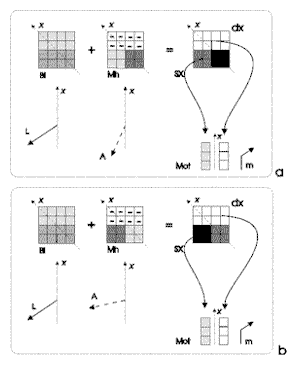
Figura 4. Riquadro a: situazione che richiede un movimento a sinistra, come in realtà avviene. Riquadro b: situazione che richiederebbe un movimento a destra per allineare L ad A. Invece il movimento dedotto dalle componenti "destra"-"sinistra" della matrice visuo-motoria è lo stesso nei due casi: il caso del riquadro b richiedeva un movimento opposto rispetto a quello del riquadro a.

Le cose cambiano se la percezione attuale della direzione della fonte di luce non è allineata con la x del sistema di riferimento egocentrico, come abbiamo visto sopra. In quel caso, infatti, non è possibile contare sulle componenti "destra" e "sinistra" della matrice visuo-motoria per ottenere un pattern motorio coerente con lo spostamento giusto per allineare la percezione attuale con quella attesa.
Per verificare questo fatto basta osservare la figura 4. Il riquadro a e quello b mostrano due situazioni che richiederebbero movimenti m opposti, in quanto nel primo caso l'angolo fra la direzione della luce attuale e quella attesa è orientato in un senso, nell'altro caso è orientato nel senso opposto. Pertanto l'unica condizione in cui si può valutare il movimento da mettere in atto in base alle componenti "destra"-"sinistra" della matrice visuo-motoria, date le due direzioni da allineare, è quella di figura 3 o di figura 1 riquadro a, in cui la direzione della percezione reale attuale coincide con la x del sistema di riferimento egocentrico, mentre quella attesa è una qualsiasi delle altre direzioni. In effetti in questa situazione sarebbe la matrice dell'homing ad "imporre" le sue componenti, in quanto quelle "destra"-"sinistra" della matrice binoculare sono uguali, essendo la direzione reale della luce "avanti".
Se la percezione attesa è a sinistra, per esempio, viene maggiormente eccitata la fila di sinistra del pattern motorio e si ha un movimento verso destra; il movimento verso destra fa si che la percezione attuale si sposti più a sinistra, nella direzione di quella attesa. Il movimento di spostamento prodotto dall'agente, infatti, ha l'effetto di ruotare il sistema di riferimento egocentrico in modo che la direzione della luce reale venga a coincidere con quella attesa, rispetto a tale sistema di riferimento.
Il modulo di allineamento deve far in modo di ruotare la matrice binoculare in modo che, per qualsiasi direzione della luce attuale, la matrice di confronto per determinare le componenti motorie sia orientata come se la direzione fosse "avanti", o zero gradi, rispetto al sistema di riferimento egocentrico. Deve anche fare in modo che la matrice di homing sia ruotata dello stesso grado, in modo che l'angolo fra le due direzioni rimanga lo stesso.
Per questo scopo è stata progettata una rete neurale ad hoc che verrà incapsulata anch'essa nel modulo dell'allineamento. Il funzionamento di tale rete verrà ora analizzato nel dettaglio.

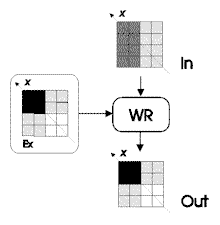
Figura 5. Schema della rete neurale di rotazione della matrice di ingresso (In) in base all'esempio (Ex). Il confronto In-Ex determina i pesi di WR in modo tale che, fornendo a tale rete in input la matrice di ingresso, essa computa una matrice coerente con l'esempio Ex.

La rete neurale visuo-motoria

Consideriamo il problema: dobbiamo fare in modo che una matrice sia ruotata in modo da coincidere con quella relativa alla direzione "avanti", ed un'altra matrice, diversa dalla prima, deve essere ruotata dello stesso grado. L'uso di una rete neurale appare quanto mai opportuno. Basterebbe, infatti, calcolare i pesi di rotazione della prima matrice e poi processare la seconda con la stessa rete. Il problema sembra quindi ridotto alla realizzazione di una rete che ruoti una matrice in modo da coincidere con una di direzione standard.
Per fare ciò c'è bisogno di un esempio, un modello preesistente della matrice con la direzione standard in modo che possa avvenire il confronto con quella da processare. La figura 5 illustra tale concetto: la matrice in ingresso In viene confrontata con la matrice di esempio Ex; da tale confronto risulta una determinata matrice dei pesi WR che, partendo dalla matrice in ingresso, computa una matrice di output Out coerente con l'esempio.
Assumere che vi sia una matrice residente, quella che abbiamo chiamato matrice di esempio, con un'attivazione statica e sempre uguale può essere visto come una deroga all'assunto della memoria locale. In effetti, come già sottolineato nel capitolo primo, nel distinguere memoria locale, memoria a lungo termine si è fatto riferimento alle componenti dinamiche. In altre parole la memoria a lungo termine che non implementiamo nel nostro sistema è quella "riscrivibile", il cui contenuto può variare. La matrice di esempio può essere considerata come un pattern di attivazione statico, così come i pesi delle connessioni dei moduli descritti fino ad ora.

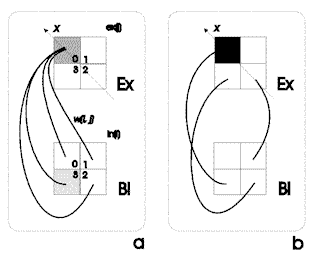
Figura 6. Esempio di rotazione della matrice binoculare Bi in base a quella di esempio Ex. Riquadro a: fase uno: determinazione del valore dei pesi. Riquadro b: fase due: trasferimento di tale valore ai pesi con indici proporzionali. La figura si riferisce al caso in cui sia maggiore di zero solo il peso w(3, 0). I pesi con gli indici ad esso proporzionali sono w(0,1), w(1,2) e w( 2,3) (riquadro b).

Scendiamo nei dettagli e andiamo a vedere come avviene il confronto fra la matrice di ingresso e quella di esempio per la determinazione dei pesi.
L'osservazione dei sistemi biologici, come sempre, ci viene in aiuto. Nel 1949 HEBB propose l'esistenza di particolari sinapsi, denominate in seguito sinapsi di Hebb. Il principio è quello per cui la forza della connessione aumenta se coincidono le attività dei neuroni connessi. Più formalmente , secondo la regola di Hebb, dati due neuroni i e j di attivazione ai ed aj rispettivamente, la forza della connessione wi,j è: wij = ai * aj
Supponiamo di avere fra la matrice di input, che sarà chiamata matrice di base, e la matrice di esempio uno strato totalmente connesso. Si considereranno 4 unità di input e 4 di esempio; ognuna di queste unità avrà l'attivazione della componente spaziale della matrice corrispondente. La matrice di esempio avrà la sola unità corrispondente alla componente spaziale "avanti" attivata, di valore uno. Si considerino i pesi delle connessioni fra le unità della matrice di base e l'unica unità attiva della matrice di esempio: tali pesi funzionano come le sinapsi di Hebb: se esiste un'attivazione sia del neurone di input, sia di quello di esempio tale peso assume il valore dell'attivazione del neurone di input moltiplicata per l'attivazione di quello di esempio. Se il neurone di esempio è attivato e quello di input no il valore del peso è zero.
In questo modo i pesi maggiori di zero sono quelli fra le componenti attive della matrice di input e quella attiva della matrice di esempio ed il valore di tali pesi è direttamente proporzionale all'attivazione dei neuroni implicati. Trasferendo il valore di tali pesi a quelli con indici proporzionali ad essi, si completa il processo.
Il procedimento è diviso sostanzialmente in due fasi. Consideriamo l'esempio di figura 6. Nella prima fase si confronta l'attivazione dei neuroni della matrice di base con l'attivazione del neurone attivo della matrice di esempio, in pratica i pesi delle connessioni fra i quattro neuroni della matrice di base con il neurone con indice 0 della matrice di esempio w(1, 0), w(2, 0), w(3, 0), w(0, 0) Secondo il principio di Hebb, la connessione attiva è quella che corrisponde a due neuroni entrambi attivati. Nell'esempio semplificato di figura 6 (riquadro a), secondo tale principio, l'unico peso attivo è w(3, 0), corrispondente alla connessione fra il neurone identificato con 3 sulla matrice di base Bi e il neurone 0 di quella di esempio Ex. Il valore del peso attivo è uguale al prodotto dell'attivazione dei due neuroni.
La seconda fase consiste nel trasferire l'attivazione dai pesi attivi agli altri pesi della rete in base al principio seguente: il valore di un peso attivo va anche a quelli il cui rapporto fra gli indici è lo stesso del peso di partenza. Nell'esempio di figura 6 il valore del peso w(3, 0) attivo nella prima fase viene trasferito ai pesi w(0, 1), w(1, 2) e w(2, 3) (figura 4.6 riquadro b). Come si può osservare essi si riferiscono sempre alla connessione di un neurone della matrice di base con il successivo, in termini di indice, della matrice di esempio.
Processando successivamente la matrice di input per mezzo delle connessioni così formate, si ha in output una matrice molto simile a quella di esempio, ma la cosa più importante è che processando una matrice diversa per mezzo della stessa rete, si ha in output una matrice ruotata dello stessa quantità della prima. La differenza di direzione che rappresentavano le due matrici prima e dopo il processamento è la stessa, ma ora una è orientata secondo la direzione standard di quella di esempio (figura 7). Le caratteristiche principali di questa rete, che per comodità verrà chiamata rete visuo-motoria, sono schematizzate nella scheda riassuntiva.

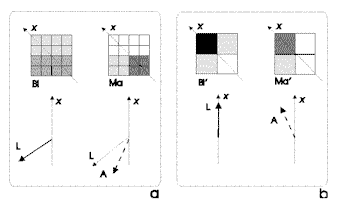
Figura 7. Il riquadro b illustra le stesse matrici del riquadro a processate dalla rete descritta nel testo. Si osservi che la differenza assoluta fra l'attivazione delle due matrici è la stessa.

Abbiamo trovato il modo per far si che tutte le possibili coppie di matrici binoculare e dell'homing siano confrontabili tra di loro, nel senso che il risultato di tale confronto sono le componenti motorie di un movimento coerente, che porti la percezione attuale a coincidere con quella attesa. Infatti le componenti motorie sono ottenute direttamente dalle componenti "destra" (90 gradi) e "sinistra" (-90 gradi) della matrice di homing ruotata in base alla rotazione della matrice binoculare rispetto alla matrice di esempio, come abbiamo visto sopra.

La figura 8 mostra lo schema globale dell'architettura del modulo di allineamento MA: esso riceve in ingresso la matrice binoculare Bi relativa alla direzione della fonte di luce attuale percepita e la matrice di homing Hom, relativa alla direzione attesa e restituisce le componenti motorie da applicare al pattern di motoneuroni Mot in modo che il movimento sia coerente con l'allineamento delle due matrici.
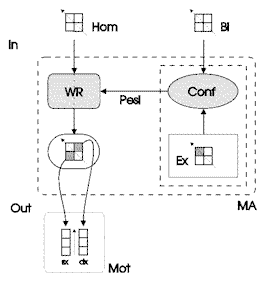
Riassumiamo il principio generale di funzionamento del modulo di allineamento, prestando attenzione alla figura 9. Il confronto fra la matrice binoculare Bi, relativa alla direzione della fonte di luce percepita rispetto al sistema di riferimento egocentrico, viene confrontata con la matrice di esempio Ex. Tale confronto permette di determinare i pesi di rotazione Pesi. Questi vengono trasferiti alla rete neurale WR, la quale processa la matrice di homing Hom ruotandola dello stesso grado della rotazione della matrice binoculare Bi rispetto alla matrice di esempio Ex. Le componenti "sinistra" (-90 gradi) e "destra" (90 gradi) della matrice di homing costituiscono le componenti per un movimento che porti la percezione attuale ad allinearsi con quella attesa.

Figura 9. Architettura del modulo di allineamento MA. Hom: matrice di homing. Bi: matrice binoculare. WR: rete neurale visuo-motoria. Conf: determinazione dei pesi di rotazione mediante confronto fra la matrice binoculare e quella di esempio Ex. Mot: pattern motorio.

A questo proposito si osservi che il valore delle componenti "destra" e "sinistra" non sono trasferibili direttamente su quelle del pattern motorio. Infatti il valore delle componenti è variabile a seconda della distanza, mentre quello delle file dei motoneuroni è zero da una parte e varia da zero ad uno dall'altra a seconda dell'orientamento dell'angolo di rotazione in ogni istante a prescindere dalla distanza. Per evitare che vi sia confusione fra i due formati è necessario quindi che le componenti computate dal modulo di allineamento si inibiscano reciprocamente. In tal modo quella minore sarà uguale a zero mentre quella maggiore sarà uguale alla differenza fra le due.

SCHEDA RIASSUNTIVA. La rete neurale visuo-motoria
La struttura di base è quella di una rete neurale ad uno strato, totalmente connessa, con 4 unità di input e 4 di output. Il principio di funzionamento di base si sviluppa sulle caratteristiche delle sinapsi di Hebb: quando l'attivazione del neurone presinaptico coincide con l'attivazione di quello postsinaptico, la forza della connessione è massima e, aggiungiamo noi, proporzionale all'attivazione dei due neuroni. Di seguito viene presentato l'algoritmo di apprendimento.
1	Si presenta in ingresso alla rete una matrice, che chiameremo matrice di base. L'attivazione di ogni componente spaziale della matrice verrà mappata su un neurone di input: in tal modo si avranno 4 neuroni in ingresso ini ognuno dei quali sta per una componente della matrice di input;
2	si confronta la matrice di base con un'altra matrice, che chiameremo di esempio. La matrice di esempio sarà anch'essa di 4 unità (2*2): ogni unità ex(j) sta per una componente spaziale. L'unica componente spaziale attiva, per definizione, è ex(j)=1;
3	si determinano i pesi w(i, 0) nel modo seguente: la dove l'attivazione del neurone della matrice di esempio coincide con quella del neurone della matrice di base, il peso è positivo ed ha valore proporzionale alle due attivazioni (regola di Hebb): w(i, 0)=in(i) * ex(j) se, invece, l'unità ini ha attivazione nulla, il peso sarà zero;
4	si trasferisce il valore dei pesi w(i, 0) a tutti gli altri pesi in modo da rispettare un principio: stessa attivazione a pesi con indici la cui differenza è equivalente. L'attivazione del peso w(0, 0) verrà propagata ai pesi w(1, 1), w(2, 2), w(3, 3), quella del peso w(1, 0) verrà propagata ai pesi w(2, 1), w(3, 2), w(0, 3), quella del peso w(2, 0) andrà propagata ai pesi w(3, 1), w(0, 2), w(1, 3) , quella del peso w(3, 0) andrà propagata ai pesi w(0, 1), w(1, 2), w(2, 3).